支持向量机

线性可分

二维图，可以用一条直线划分开

线性不可分

二维图，不可用一条直线划分开

多维空间

超过三维，就需要用超平面划分，需要用到数学知识

支持向量机条件

使用MARGIN最大这个条件并不能唯一确定一条直线
该直线应满足

  • 该直线分开了两类
  • 该直线最大化了间隔
  • 该直线处于间隔的中间，到所有支持向量距离相等

线性可分条件下-支持向量机优化问题

假定训练样本集是线性可分的
支持向量机需要寻找的是最大化间隔的超平面

最小化：w是一个向量，和线代求值一样，求出w的平方

事实一

事实二


支持向量机优化问题推导中最难理解的部分
用a去缩放wb

（ w，b）表示的超平面和（ aw， ab）表示的超平面是同一个平面
因此可以用参数a去缩放（ w ，b）
所以根据事实二，支持向量X0到超平面的距离将会变成：

最大化支持向量到超平面的距离 等价于最小化 |w|

优化问题定义为

最小化：二分之一 |w| 的平方
最小化： |w|

限制条件

支持向量到超平面的距离为：二分之一 |w|
在非支持向量上

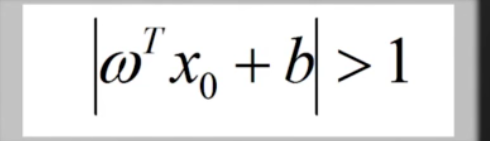
二次规划

（1） 目标函数（Object Function) 是二次项
（2）限制条件是一次项


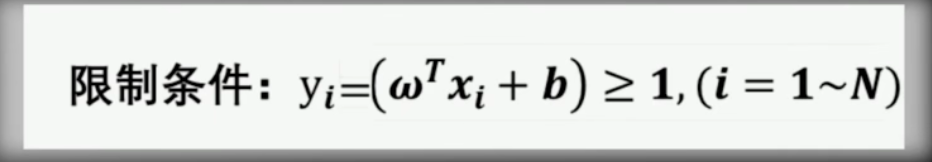
要么无解，要么只有唯一的最小值

线性不可分问题

对于线性不可分的情况下，需要设当放松限制条件

线性不可分下的最优化